“知之者不如好之者，好之者不如乐之者”。 ——《论语·雍也》
乐之者，大才也！乐之者，吾辈意欲所致也！
“一口气了解国债”系列前言
本系列文章力图梳理出相对完整的国债知识脉络，以非专业视角，进行一般性科普。期望借此，能帮助到更多希望学习了解国债，却苦于在散落零星，庞杂繁复的信息中难以找到切入点的读者。
按知识脉络，整理了本系列文章的思维导图，读者可以按图索骥进行阅读。
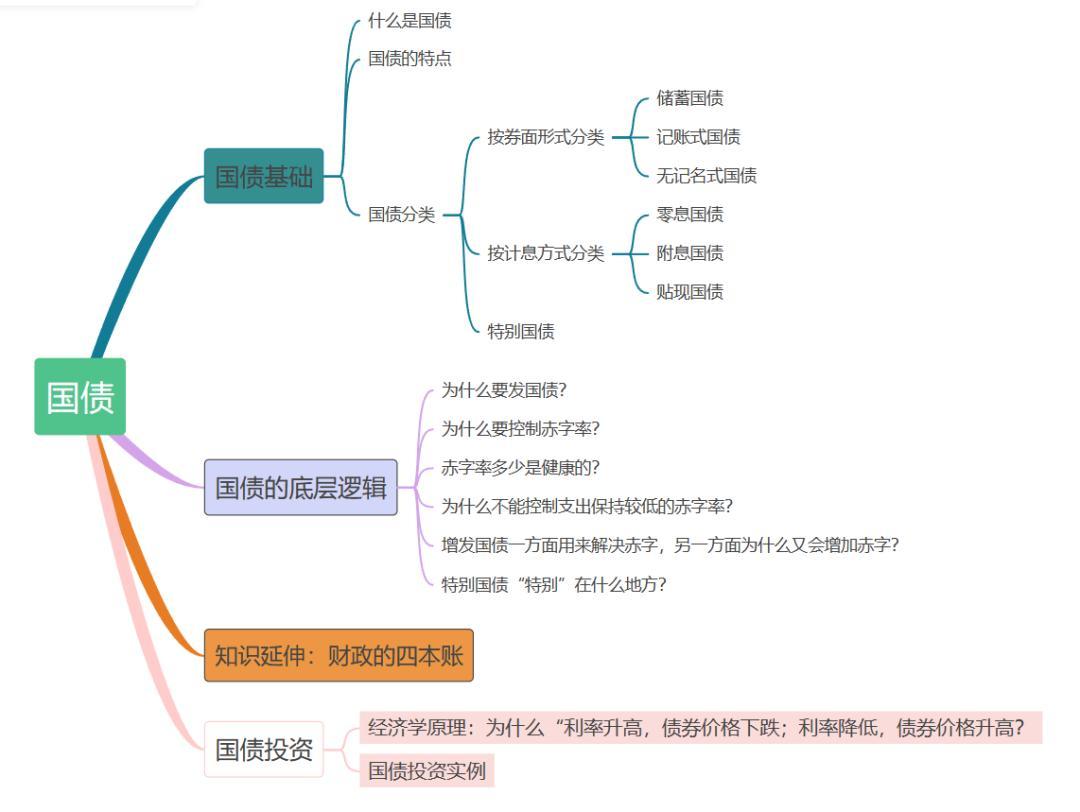
系列文章前文：
《硬核！系列文章带你从零开始了解国债（一）——什么是国债》
《硬核！从零开始了解国债（二）——6个问题带你渐次递进了解国债的底层逻辑》
《硬核！数据详解财政“四本账”》
按照系列文章思维导图，本文将详细阐述一个重要的和债券相关的经济学原理——利率与债券价格呈负相关的关系，即：当利率上升时，债券价格下跌；当利率下降时，债券价格上涨。
在写作之前，关于上述问题，我检索了一下网上的解答，用“供需关系”的逻辑来回答上述问题，是一种普遍被大众接受的观点。具体如下：
当利率上升时，将要新发行的债券因为高利率吸引更多的购买者，相比之下已发行流通的债券因为利率低，吸引力减弱，需求减少，导致价格走低。反之亦然。
要用供需关系来解释上述问题，必须明确其中暗藏的几个限定条件：
1、将要新发行的债券。将发未发，预期在了，手上持有低利率债券的人，就会抛售现有债券，腾出资金，准备购买利率更高的新债券。因此，旧债券吸引力降低，需求减弱，价格走低。
2、利率对价格负相关关系是对于“旧债券”而言，新债券不适用。否则上述的解释将存在致命的逻辑漏洞——新债券利率高，需求量大，价格升高。明显存在不能自洽的逻辑问题。
还有一个版本，抛弃新旧债券的概念，无论新旧，统一称为债券，并且在债券之外，引入银行存款的概念。具体解释如下：
假设市场上的资金只能投资银行储蓄和债券。
当市场利率上升，银行存款的利率也随之上升，投资者会将资金放入银行吃利息，那么债券市场的资金变少，购买债券的人变少，债券的买卖价格下降。
反之，当市场利率下降，银行存款的利率也随之下降，投资者会将资金从银行取出购买债券，那么债券市场的资金变多，购买债券的人变多，推动债券的买卖价格上升。
这个版本个人认为概念更加清晰，逻辑更加顺畅，理解起来相对容易！
至此，用供需关系，大致能够解释债券价格与利率的负相关关系了。
如果能听懂上述的解释，那么恭喜你，你已经找到答案了，并对基本的经济学原理有了一定的认识。
有了疑问，寻找答案，搞清楚答案，这样的人我们称之为“知之者”！
“知之”偏重于理性，对象外在于己，你是你，我是我，往往失之交臂，不能把握自如！
“好之者”，对所知之事产生更加浓厚的兴趣，由表及里，他们往往愿意投入更多的时间和精力，对事物喜欢刨根问底，喜欢从不同的视角分析，挖掘其中更深层次内涵！
“乐之者”，不仅能知学，好学，更能乐学。这类人，往往能够将所学，所见融会贯通，理论实践有机融合，真正达到乐在其中的境界！而由乐在其中所催生出的内在驱动力，将会使他们能够持续不断地进步和提升。
乐之者，大才也！
为了能够向“好之者”，“乐之者”看齐，本文将尝试透视供需关系，分析其中潜藏的更深层的原理及逻辑！
好了，大道理讲了一堆，开始入题！
讲利率与债券价格之间的关系，我们从时间开始说起！
时间的魔力：时间就是金钱
在经济领域，金融市场中，“时间就是金钱”不是一句口号，而是真真切切，看得清摸得着的。
举个例子。
假设你现在有100块钱，当前银行的利率为10%，那么这100块钱存到银行，那么一年后你的100块钱就会变成110块。
进一步拉长时间，第2年，第3年，…第10年后，这100块钱分别是：121元，133元，...，259元。计算的方法很简单：
第一年：100 * (1+0.1) = 110
第二年：100 * (1+0.1)2= 121
第三年：100 * (1+0.1)3= 133
…
第10年，100 * (1+0.1)10= 259
第n年：100 * (1+0.1)n
若n=30，则第30年，这100块钱的价值为100 * (1+0.1)30= 1745元。
30年，你手里的100元变成了1745元，足足17.45倍。
这30年间，你唯一需要做的事情就是吃饭，睡觉，然后就能躺着数钱。
这不是你辛勤劳动换得的报酬，也不是你凭借着卓越的投资天赋驰骋于资本市场斩获的筹码，你做的唯一事情聘请时间成为了你的理财顾问，然后你大手一甩，优哉游哉去了。
这是对“时间就是金钱”最具象化的解释。
讲到这里，感觉事情怪怪的：“每天什么都不用做，仅仅靠时间就能时间财富的增长？”。
从小的教育告诉我们，没有辛勤的劳动付出，是不可能有回报的。
经济学原理也告诉我们：劳动报酬是劳动者付出体力或脑力劳动所得的对价，体现的是劳动者创造的社会价值。
“不劳而获”可不是一个褒义词！
事出蹊跷必有妖！
时间的魔力：现在的100元，在未来不值100元
我们以天下没有不劳而获的价值观为指导，揭露上述分析中的“陷阱”。
在上述例子中任何一个时间段内，你并没有付出任何劳动，按照劳动与报酬等值的概念，一年后你的110块钱，理应与今天的100块钱在价值是相等的。
再具体一些，考虑通货膨胀，物价上涨，货币贬值的事实：
假设今年大米是2元一斤，那么今年你用100块钱能买到的大米数量为50斤。
再假定物价上涨率为10%/年，那么第二年实际大米的价格为：
2元 * (1+ 10%)= 2.2元
第二年能买到的大米数量为：
110元÷2.2元/斤 = 50斤。
在你饭量并没有减少的情况下，虽然你的资产增值了，但是他还是只能为你提供50斤大米，并不能多养活你几天。
换句话说，你在第二年时手里拥有100块钱，折合到今年来看，这100块钱仅仅相当于现在的90.9元钱。
100÷(1+10%)=90.9元
90.9元称为“现值”！
未来的100元钱，折合到现在不值100元钱，这就是经济学中最重要的概念之一：折现。
折现，Discounting the Future：
Discounting：打折
Future：未来
Discounting the future，直译就是“将未来打折”。
为了更明确的体现未来和现在两个时间点，再扩展一下名词：Discounting the Future to Now。
Now：当前，现在的意思，即将未来打折到现在。
折现，又称“贴现”，其中用于折现计算的数值10%，就是折现率。
折现率可以是无风险利率，可以是到期收益率，也可以是到期回报率。
真实的折现率要考虑的因素很多，估计方法也很多，总的来说，应该和投资者的预期回报相关。
分析到这里，庆幸庆幸，没有“不劳而获”的价值观可算没有塌方。
折现的应用：资产估值写了这么多公式，算了这么多数字，讲了这么多术语，就学到了一个“折现”的概念。折现到底有什么用处？不仅有用，而且大有用处！说一个大多数人都很感兴趣的话题，资产估值。如“债券估值”，“公司企业估值”，还有大家特别感兴趣的对“股票估值”！我们拿股票估值来说明折现的应用！无论一级市场，二级市场流通的股票要想成交，必须有价格一说。“低买高卖”是每个投资参与者所孜孜追寻的交易真谛。
“低买高卖”说起来简单，做起来难！首先面临的第一个问题就是“比大小”。谁和谁比？经济学原理告诉我们：价格是价值的货币表现，是商品价值的外在形式！因此，需要比较的是：当前的价格和其真实的价值！当实际价格低于其真实价值时，我们称该资产当前被“低估”！如果你相信经济学基本规律：“价值决定价格，价格围绕价值波动”（记住这句话，后面要用！！！），
那么长期来看，价格总体上会与价值相符，被低估的资产有回归其真实价值的向上驱动力，因此被低估的资产是有买入价值的！反之，当股票的实际价格高于其真实价值时，我们称之为被“高估”！此时处于高风险区位，如果你仍然相信基本的价值与价格的内在规律，那么大概率你此时一定会管的住手，不会贸然买入！
那么一个公司的股票真实价值到底来源于哪？应该如何进行估计计算？持续盈利是一个公司经营永远追求的目标，因此公司的价值体现在公司持续盈利的能力。如何把公司持续盈利能力转换为公司的价值？我们简化场景，不考虑公司的固定资产，非经常性损益等其他因素，只看主营业务净利润收入。
假设公司第一年预期利润为100万元，第二年预期利润为200万元，第三年为350万元，第四年为550万元.......将每年利润逐一罗列：第一年：100万第二年：200万第三年：350万第四年：550万......是不是很熟悉的感觉？在分析“时间就是金钱”的部分，我们给定利率，计算并罗列了未来每年的资产。我们又已经知道了这样一个基本的常识：“未来的100元不如现在的100元值钱”。因此，接下来，要干什么？折现！！！要想折现，还缺少一个计算的条件，即我们上文中提到的折现率！好办，假设我们投资的预期投资回报率为5%，那么就可以用这个5%进行折现计算了。折现后：第一年：100 ÷(1+0.05) = 95.24万
第二年：200 ÷(1+0.05)2= 181.41万
第三年：350 ÷ (1+0.05)3= 302.34万
第四年：550 ÷(1+0.05)4= 452.49万
......
简单起见，我们只看前4年折现后加和的总价值为1031.48万元。假设该公司流通股数量为1000万股，则每股平均价格大约为1.03元。这个1031.48万元就是公司当前的价值，又称“市值”，而1.03元则体现的是当前公司每股股票的价值。因此，“比大小”的标准就出来了！若当前股价低于1.03元，则此时股价处于低估状态；若当前股价高于1.03元，则此时股价处于高估状态。上述的过程就是大名鼎鼎的现金流折现估值模型（DCF，Discounted Cash Flow）。
DCF估值模型基于这样一个理念：企业的价值等于其未来现金流的现值总和。它考虑了货币的时间价值和企业成长、持久经营和风险因素，是一种评估公司或资产价值的重要财务模型！
我们从时间开始，引出了经济学中最重要的概念之一：折现。
明白了折现的概念，后续的问题分析的难点及障碍已基本扫清。
我们通过折现公式，以及在本系列文章中提到的息票国债的例子，来推导证明债券价格和利率的关系。
我们在国债系列的第一篇文章中，提到了记账式付息国债，再回顾一下要点。债券面值：发行时债券的价格。
票面利率：票面利率和债券面值共同决定债券的利息：
债券面值×息票利率 = 利息。
附息国债，又称息票国债或付息票国债，分期付息，到期还本！
上述内容详见：《硬核！系列文章带你从零开始了解国债（一）——什么是国债》
为什么特意提到记账式付息国债？价格跟随市场的变化围绕价值波动，因此对于国债或者其他类型的债券而言，必须是在市场上可流通，可交易才有价格波动。与记账式国债不同，凭证式国债不能上市交易，提前兑取时的价格不随市场利率的变动而变动，可以避免市场价格风险。债券市场价格的变动不会影响凭证式国债的收益。我们以面值为1000，票面利率为10%的10年期附息国债为例，并设定几个不同的利率水平，分别为7.13%，8.48%，10.00%，11.75%，13.81%，分别计算不同利率水平下，债券的价值。按照付息国债的还本付息以及折现的原理，以7.13%利率为例，计算过程如下：每期利息收入：1000*7.13% = 71.3元。假设按年支付利息，则10年期间每年需要支付利息71.3元。10年后到期，还本1000元。按照折现的思路，分别将10年中每年的利息折现，并且1000元本金也是第十年偿还，所以也要折现，因此两部分折现后累加，就可以得到国债的价值。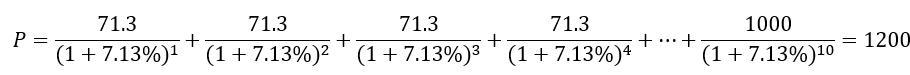
按照相同的计算方式，将其它利率代入公式计算后，分别得到不同利率下对应的折现值，如下：
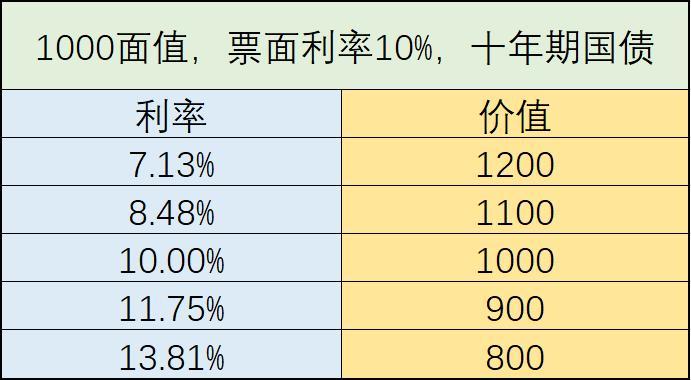从上表的结果可以看到：利率越高，表明未来息票利息支付与最终偿付折现到当前的价值越低。由此，我们可以继续推论：1. 利率越高，折现后现值越低；2. 因为价格是价值的外在表现：所以价值越低，则价格越低；因此，综合1 2 两点，可以得到“利率越高，债券价格越低”。反之亦然。至此，我们由基本的经济学原理出发，理论结合实际，从本质上揭示了“债券价格与利率成反比的关系”的内在逻辑。上表中，还有一个有意思的现象。假设我们是在10%利率下，以1000元面值买入的国债，以此为原点，看一下利率波动带来的影响。1. 假设买入后，利率升高，由10%提高至13.81%，如果此时我们卖出，则国债的价格仅有800元，与最初买入相比，一下子损失了200元。2. 又假设买入后，利率降低，由10%降低至7.13%，如果此时卖出，则此时国债的价格为1200元，与最初买入相比，净赚了200元。从上面的例子中可以看到，利率变动会导致长期债券的投资风险变得非常大，这就是债券投资中的“利率风险”。
最后，找了一张图，大家可再次直观体验一下“债券价格与利率呈负相关”的关系。下图是美国10年期国债价格2024年6月~2024年11月价格走势图，其中9.18日，美债价格触底反弹，一路走高。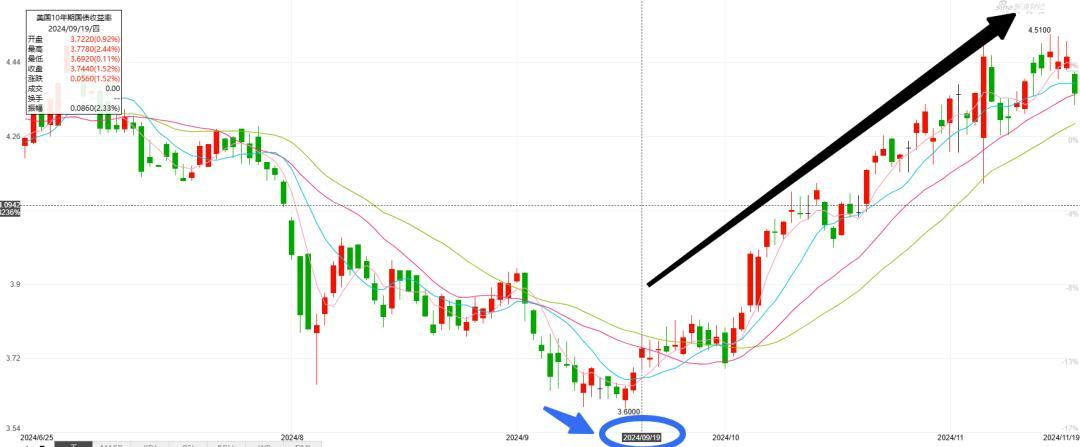
9.18日发生了什么？查了一下当天的新闻：“2024年9月18日，美联储在最新政策会议上宣布将联邦基金利率目标区间下调50个基点至4.75%-5.00%，为四年来首次降息”。降息之后，美国10年期国债价格应声持续走高！
F：察言观行
#A股上演放量深V，调整结束了？#$信用债ETF博时(SZ159396)$ $30年国债指数ETF(SH511130)$ $国开ETF(SZ159650)$
本文作者可以追加内容哦 !
